Graph Of Absolute Value Function

Graphing Absolute-Value Functions

Virtually functions are not straight lines, then you should wait to need to know how to graph the absolute values of quadratics, cubics, and other types of functions. Fortunately, the process for graphing absolute-value functions involving arguments which are curvy lines is exactly the same equally for accented-value functions whose arguments are nicely linear plots. In other words, you'll be doing the regular graphing process, but you'll probably be flipping role of the "regular" graph (that is, the graph of the office within the absolute-value confined) over the 10 -axis.

Content Continues Beneath

The simplest non-linear function is a quadratic, which commonly graphs as a parabola. If any portion of that parabola crosses the x -axis, then the absolute-value bars will flip that portion over that centrality.

Graph y = |x ² − iiix − 4 |

Inside the accented-value bars of this function, I've got a quadratic. Without the absolute-value bars, the graph of the quadratic inside the bars is a generic parabola.

I tin confirm (past factoring) that the x -intercepts are at x = −1 and x = iv. I tin use a formula to confirm that the vertex is at (1.five, −6.25). The y -intercept is at y = −iv.

The "regular" parabola'south graph looks like this:

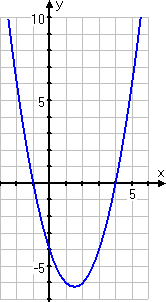
graph of y = x^2 − 3x − 4

Between the ii ten -intercepts, the graph goes below the 10 -centrality, which ways that the output values from the function (that is, the y -values) are negative. Merely the quadratic is inside accented-value bars, and those confined volition flip that negative part in the middle, redrawing that portion to exist higher up the x -axis. So I should expect the graph to look similar this:

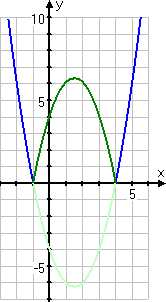
graph with below-axis portion of parabola now shown in faint green, and flipped-over-the-axis portion drawn above the axis in dark green

Then at present I have a good thought of what I should expect my absolute-value graph to be. (I did the above "thinking" on scratch-paper; it will non exist role of my hand-in answer. But doing this pre-check is very helpful, by reinforcing what I've learned previously.)

Hither's my T-nautical chart:

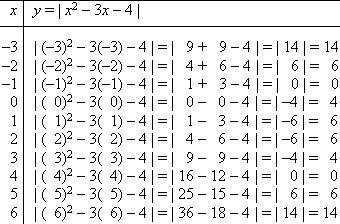
T-chart with computations leading to points (−3, 14), (−2, 6), (−1, 0), (0, 4), (1, 6), (2, 6), (3, 4), (5, 6), and (6, 14)

I've got two consecutive ten -values with the aforementioned y -value. This doesn't mean that there's a horizontal line between (1, 6) and (2,−6); instead, it ways that the vertex is halfway between these two x -values, and a piffling flake above the y -values. I'll want to be careful to draw a nice arc betwixt these two points.

My graph looks like this:

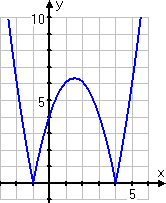
graph of y = | x^2 − 3x − 4 |

Graph y = |x ³ − vx ⁱⁱ + 6x |

They've given me the absolute value of a cubic. From what I know about the behavior of polynomials, I know that the cubic within the absolute-value bars comes upwardly from the bottom, maybe flexes a flake in the middle, so heads upwards forever. Since I'll be using the absolute values, I know that the left-hand segment of the graph will be flipped up and over the x -centrality.

I can find the 10 -intercepts by factoring.

ten ⁱⁱⁱ − five10 ² + half dozenx = 0

10 (ten ² − 5x + 6) = 0

x (x − 3) (x − 2) = 0

x = 0, 2, 3

I'll demand some additional plot points, to be certain of where the graph is going. My T-chart, without the computations, is:

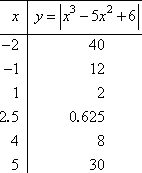
T-chart with points (−2, 40), (−1, 12), (1, 2), (2.5, 0.625), (4, 8), and (5, 30)

Together with the intercepts that I found, my graph ends up looking like this:

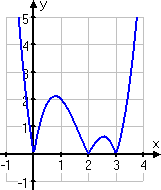
graph of y = | x^3 - 5x^2 + 6 |

If at that place had been no absolute-value confined on the role to a higher place, then the first and third segments of the line in my graph would have been below the x -axis. The accented-value confined forced those two segments above the axis. If you're ever at all in doubt of where the graph should be going, take the time to plot some more points (such every bit the (ii.5, 0.625) point I found to a higher place) so you can be certain of your answer before you paw information technology in.